A royal flush consists of a certain five cards of the same suit. Assume we are dealt one of these cards. Then the suit is determined, and we now need the remaining four cards of that suit. So, let's take the probability of being dealt one of the certain five cards (10, J, Q, K, A) of any suit. Since there are five such cards per suit, and there are four suits (the set of suits is \( \{ \diamondsuit, \heartsuit, \clubsuit, \spadesuit \} \)), then we can get any one of those cards to start building a royal flush. Therefore, the probability of getting a starting card is \[ P(\text{starting card}) = \frac{20}{52}. \] Once we have a starting card of a certain suit, our suit is restricted. That is, we may only get the remaining four cards from the same suit as our starting card. Then the probability of getting one of the four cards from the same suit is \[ P(\text{one of the four from the same suit}) = \frac{4}{51}. \] Likewise, after we get the second card, there are three left to get, so the probabilities are \( 3/50 \), then \( 2/49 \), and then \( 1/48 \). What, then, is the probability that we will get all of the necessary cards? It is the product of all these probabilities: \[ P(\text{all}) = \frac{20}{52} \cdot \frac{4}{51} \cdot \frac{3}{50} \cdot \frac{2}{49} \cdot \frac{1}{48} = \frac{1}{649\,740} = 1.539\ldots \times 10^{-6} = 0.000\,153\,9\ldots \%. \] Not very good odds.
Monday, June 20, 2011
How Likely Are You to Be Dealt a Royal Flush?
Saturday, June 18, 2011
Calculating the Number of Trailing Zeros in a Factorial
The factorial function, denoted \( n! \), where \( n \in \mathbb{Z}^* \), is defined as follows: \[ n! = \begin{cases} 1 & \text{if $n = 0$,} \\ n(n - 1)! & \text{otherwise}. \end{cases} \] In the case of \( n = 10 \), \( 10! = 3\,628\,800 \). Note that that value has two trailing zeros. When \( n = 20 \), \( 20! = 2\,432\,902\,008\,176\,640\,000 \) and has four trailing zeros. Can we devise an algorithm to determine how many trailing zeroes there are in \( n! \) without calculating \( n! \)?
Let us define a function \( z : \mathbb{N} \to \mathbb{N} \) that accepts an argument \( n \) that yields the number of trailing zeros in \( n! \). So, using our two examples above, we know that \( z(10) = 2 \) and \( z(20) = 4 \). Now, what is \( z(100) \)?
An integer \( a \) has \( k \) trailing zeros iff \( a = b \cdot 10^k \) for some integer \( b \). Now, the prime factors of \( 10 \) are \( 2 \) and \( 5 \). So, what if we consider the prime factors of each factor in a factorial product? For example, consider the first six terms (after \( 1 \)) of \( 100! \) and their prime factors. We omit \( 1 \) because of its idempotence: \[ \begin{align} 2 &= 2 \\ 3 &= 3 \\ 4 &= 2^2 \\ 5 &= 5 \\ 6 &= 2 \cdot 3 \\ 7 &= 7 \end{align} \] We see that \( 7! \) contains one \( 5 \) and (more than) one \( 2 \). Therefore, \( 7! \) contains a factor of \( 10 \), so we should expect there to be one trailing zero in \( 7! \). And we see that \( 7! = 5040 \), which does indeed have one trailing zero. This suggests that we could, for any integer \( n \) in \( n! \), cycle through the integers from \( 2 \) to \( n \), finding the prime factorization of each integer, and counting pairs of \( 2 \) and \( 5 \) that we find.
You might have noticed from our example of \( 7! \) that there are four \( 2 \)s and only one \( 5 \). Consider that there are \( n/2 \) even factors in \( n! \)—that is, every other integer factor of \( n! \), starting at \(2\), is even. So there are \( n/2 \) even factors. Each of these has at least one \( 2 \) in its prime factorization, and many of them have more than one. Now consider how many factors of \( 5 \) there are in \( n! \): there are, in fact, \( n / 5 \). So, we can see that, for every \( 5 \) we find in \( n! \), there is a \( 2 \) we can match with it. This suggests that we only need count the \( 5 \)s and not the pairs of \( 2 \) and \( 5 \).
This now suggests an algorithm, presented here in Java:
Using this algorithm, we find that \( z(100) = 24 \).
Friday, June 10, 2011
Adobe Reader's Big Problem
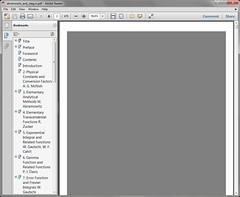
I use PDFs often. Nothing excels them in fidelity of design to documents for which design is important. The Adobe Reader, in its 5.5 days and earlier, was the standard PDF reader of choice. But with version 6, serious bloat occurred, and Adobe Reader is only now, in its latest versions, recovering from that problem. I have a new problem with Adobe Reader, though. Take a look:
This is a document that appears to be made of scanned images placed in text pages, produced by \( \mathrm{\TeX} \). Note how the scanned images appear as completely useless gray boxes. Here is how the document should look, and does look, in other PDF viewers:
I have searched and searched on this matter, but the results are few and old, and whenever I try to employ a solution I do find, it doesn't work.
Monday, June 6, 2011
Generate a Zero-Valued UUID
Say you want a UUID of 00000000-0000-0000-0000-000000000000, but you just want to make one fast, without having to find out the number and grouping of digits. Here's a way to do it: